AlcaSAT
06 Nov 2014Alcazar is a new pen and paper puzzle game created by the incredible game company. I first heard about Alcazar when Jonathan Blow posted about his interest in the game:
These puzzles are pretty neat: http://t.co/cAy4KFL5j9
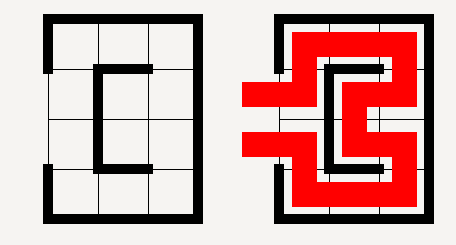
— Jonathan Blow (@Jonathan_Blow) May 20, 2014On the game's website you can try out some example games for free. The goal of the game is to draw a single path through a maze that visits every cell of the gamefield. The maze also has openings on its boundary and you have to enter in one and exit in another. Furthermore you are not allowed to cross your path.
The puzzle reminded me of my thesis, so I tried to implement a solver for it. First up was the representation of the game in a 2-dimensional array.
x x x x x x x
x 0 - 0 - 0 x
x | x x x | x
- 0 x 0 - 0 x
x x | x x
- 0 x 0 - 0 x
x | x x x | x
x 0 - 0 - 0 x
x x x x x x xIn this representation every cell is represented by a 0, a wall by a x, a line segment which is set by | or - and an unset line segment by an empty space.
Notice that most of the entries in the array aren't necessary to consider for a solver algorithm because we only care about which lines are set or not.
In fact we only care about the array items \( \{ (i,j) \mid mod(i,2)=1 \oplus mod(j,2)=1\} =\) \( \{ (1,0), (0,1), (1,2), (2,1), (3,0), (0,3), ... \} \).
SAT-solving
SAT is the problem of finding a satisfying assignment of a (in this case boolean) logic formula. Here is an example of a boolean formula: \[ f = (x \to y) \wedge (\neg x \vee y) \]
The operators of boolean formulas are \( \{ \wedge \text{(and)} \) , \( \vee \text{(or)} \) , \( \to \text{(implication)} \) , \( \neg \text{(not)} \} \) and \( \{ x, y, ..\} \) represent variables in the domain \( \{true,false\} \). An assignment is just a function which assigns every variable a truth value.
\[ a(x) \to true, a(y) \to false \]
With a formula and an assignment you can evaluate the truth value of the formula by first replacing the variables with their truth values and then using the truth table of the operators recursively:
\[ a(f) = a((x \to y) \wedge (\neg x \vee y))= \\ a(x \to y) \wedge a(\neg x \vee y) =\\ (a(x) \to a(y)) \wedge (a(\neg x) \vee a(y)) = \\ (true \to false) \wedge (\neg true \vee false)=\\ false \wedge (false \vee false)=\\ false \wedge false=\\ false \]
As was shown the formula \( f \) with the assignment \( a \) evaluates to \(\text{false}\). An assignment \( a \) of \( f \) is called satisfying if and only if \( a(f)=true \). In the example above a satisfying assignment is \(a(x)=true, a(y)=true \). The problem of finding such a satisfying assignment is hard but there exist free solvers which solve formulas with million of variables in a matter of seconds.
You might ask yourself how this process might solve Alcazar puzzles. Well let's try it with a simpler example: You want to know if the grass is wet and you know that it is wet when it rains. First you decide which variables you have in the statement: \( wet \text{(the grass is wet)} \) and \( rained \text{(it rained)}\). It is important that the variables can only be \(true\) or \( false \). Next you define a formula which captures the dynamics of the system: \( rained \to wet \). Now we can find satisfying assignments of the formula when we know that it has rained: \[ rained \wedge ( rained \to wet ) \] The formula reads like this: "it rained AND (IF it rained THEN wet)".
Now we hand the formula to our SAT-solver which spits out \( a(rained)=true, a(wet)=true \) and we know that it rained and the grass is wet. The process of defining the meaning of the variables and generating the formula is called encoding.
Encoding Alcazar puzzles
x x x x x x x
x 0 - 0 - 0 x
x x x x x
0 x 0 0 x
x x x | x
0 x 0 0 x
x x x x x
x 0 0 0 x
x x x x x x xIn the Alcazar puzzle we have line segments which can be either turned on or off. They are therefore a perfect candidate for the set of variables \( \{x_{i,j} \mid puzzle_{}(i,j)=\text{'} \enspace \text{'} \} \). Here's an example of a puzzle where \( a_{}(x_{2,1})=true\), \( a_{}(x_{4,1})=true \) , \( a_{}(x_{5,4})=true \) and for all other \( a_{}(x_{i,j})=false \).
Now we need to generate a formula given a puzzle. To make things easier later,
we define a helper function \( two( x_{0}, ..., x_{n-1})\) which takes
as an input \( n \) variables and outputs a formula which is satisfiable if and only if
2 of the variables are assigned the \( true \) value. In math :
\[ a(two(x_{0}, ..., x_{n-1})) = true \\ \iff \\
\rvert \rvert \{x_i \mid a(x_i) = true\}\rvert \rvert = 2 \]
The formula is constructed by generating all combinations of the variables and only leaving 2 variables normal and negating the rest. We join the combinations with the \( \vee \text{(or)}\) operator: \[ two(x_{0},...,x_{n-1}) = \\ \bigvee_{i<j} (x_{i} \wedge x_{j} \bigwedge_{k \notin \{ i,j \}} \neg x_{k}) \]
Here's an example of generating the formula for 3 variables and all the satisfying assignments \[two(x_0,x_1,x_2) = (x_0 \wedge x_1 \wedge \neg x_2) \vee \\ (x_0 \wedge x_2 \wedge \neg x_1) \vee (x_1 \wedge x_2 \wedge \neg x_0) \\ \begin{array}{c|lcr} a_i(x) & x_0 & x_1 & x_2 \\ \hline a_0 & true & true & false \\ a_1 & true & false & true \\ a_2 & false & true & true \end{array} \] As expected in all the satisfying assignments the number of variables which were assigned the \( true \) value was 2. Equipped with this new function we can now tackle the problem of generating a formula for Alcazar puzzles. Our 2 requirements for our formula are
- Exactly 2 exit lines have to be active
- Every cell has exactly 2 active neighbouring line segments
These 2 requirements ensure that we generate a valid path. Consider that the number of lines in a cell is:
- 0, the cell never gets a visit, so the whole solution would be wrong.
- 1, one line enters the cell but never leaves it, which means that the path would end in this cell.
- 2, one line enters the cell and another one leaves the cell. This is what we want.
- 3 or 4, too many lines enter the cell, which means that we generate a crossing in the path.
# Some examples for number of lines in a cell
# 0 1 2 3 4
x x x x x x x x x | x
0 0 - 0 - - 0 - - 0 -
x x x x x | x x | x x | xThe formulas for the requirements are \[ two( \{ x_{i,j} \mid x_{i,j} \in exits \}) \\ {\Large\forall}_{cell} two(neigh(cell)) \] where \( neigh(cell) \) returns a set of neighboring line segments of the cell which are not walls and \( exits \) is the set of all lines which are on the boundary of the puzzle. In the example above \( neigh(1,1) = \{ x_{1,2} , x_{2,1} \} \) and \( exits= \{ x_{0,3}, x_{0,5} \} \). Basically we are now done: Given a puzzle we find the exits and generate the first formula, then we visit every cell, generating the second formula and finally join all the formulas with the \( \wedge \text{(AND)}\) operator. This formula is descriptive enough to generate correct solutions for small puzzles like the one above but problems arise if we feed our algorithm bigger puzzles.
The loop problem
We observe that our requirements were not descriptive enough after all. The problem is that we never encoded that there should be only one path. To solve this problem we could define a formula which expresses that every line should be reachable by one exit. This would guarantee that there is only one path in the assignment. To encode such a reachability constraint we would have to encode every possible path in a smart way ( I covered one of them in my bachelor thesis). A simpler approach is to use the SAT-solver to quickly generate possible assignments, analyze them with a non-SAT technique and then feeding the new information back to the formula. This technique is called a hybrid-approach and uses the best of both worlds (quickly generating possible solutions and enforcing complex constraints).
Hybrid-solving
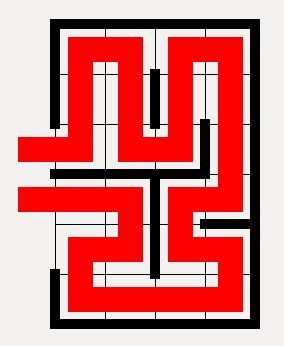
The Hybrid-solver for Alcasat works by generating a possible assignment as usual and then finding all loops in the generated solution. In the example above it would find one loop in the left upper corner: \( loop= \{ x_{1,2}, x_{2,1}, x_{3,2}, x_{2,3} \} \). For every loop it now generates a new formula \( \bigvee_{l \in loop} \neg l \) which gets added to the already existing formula. These new loop formulas guarantee that in the new solutions there can't exist the same loop again. We repeat this process of SAT-solving and loop finding until we find a solution without loops.
Implementation
AlcaSAT was implemented in python and I used minisat for the SAT-solving part. Creating the GUI was easy due to the pipeline I used:
- create a
*.uifile with qtdesigner, a WYSIWYG editor for GUI's - use pyside-uic to convert the
*.uifile to a python script - importing the generated python files into the
controller.py
Here's a demo of the application:
If you want to build AlcaSAT yourself, you need minisat and
pyside-uic in your environment.
sudo apt-get install minisat
sudo apt-get install pyside-tools
Then you should be able to run
git clone https://github.com/david-westreicher/alcazar
cd alcazar
make
python src/alcazar.py